Queuing theory: Definition, history & real-life applications & examples

Queuing theory is a powerful tool to analyze the daily phenomenon of waiting in line. Discover how to define queuing theory, how it started, why it’s important, and how it can be applied to real-life situations.
1. What is queuing theory?
2. How did queuing theory start?
3. What are the different types of queuing systems?
4. Why is queuing theory important?
5. The application of queuing theory & queuing theory examples
6. How does queue psychology impact queuing?
Queuing theory refers to the mathematical study of the formation, function, and congestion of waiting lines, or queues. It’s also referred to as queueing theory, queue theory, and waiting line theory.
At its core, a queuing situation involves two parts:
- Someone or something that requests a service—usually referred to as the customer, job, or request.
- Someone or something that completes or delivers the services—usually referred to as the server.
To illustrate, let’s take two examples. First, when looking at the queuing situation at a bank, the customers are people seeking to deposit or withdraw money, and the servers are the bank tellers.
Second, when looking at the queuing situation of a printer, the customers are the requests that have been sent to the printer, and the server is the printer.
Queuing theory scrutinizes the entire system of waiting in line, including elements like the customer arrival rate, number of servers, number of customers, capacity of the waiting area, average service completion time, and queuing discipline.
Queuing discipline refers to the rules of the queue, for example whether it behaves based on a principle of first-in-first-out, last-in-first-out, prioritized, or serve-in-random-order.
Queuing theory was first introduced in the early 20th century by Danish mathematician and engineer Agner Krarup Erlang.
Erlang worked for the Copenhagen Telephone Exchange and wanted to analyze and optimize its operations.
He sought to determine how many circuits were needed to provide an acceptable level of telephone service, for people not to be “on hold” (or in a telephone queue) for too long. He was also curious to find out how many telephone operators were needed to process a given volume of calls.
His mathematical analysis culminated in his 1920 paper “Telephone Waiting Times”, which contained some of the first queuing models and served as the foundation of applied queuing theory.
The international unit of telephone traffic is called the Erlang in his honor.

Image via Reddit
Queuing theory uses the Kendall notation to classify the different types of queuing systems, or nodes. Queuing nodes are classified using the notation A/S/c/K/N/D where:
- A is the arrival process
- S is the mathematical distribution of the service time
- c is the number of servers
- K is the capacity of the queue, omitted if unlimited
- N is the number of possible customers, omitted if unlimited
- D is the queuing discipline, assumed first-in-first-out if omitted
For example, think of an ATM. It can serve:
- One customer at a time
- In a first-in-first-out order
- With a randomly-distributed arrival process and service distribution time
- Unlimited queue capacity
- Unlimited number of possible customers.
Queuing theory would describe this system as a M/M/1 queuing model (“M” here stands for Markovian, a statistical process to describe randomness).
Queuing theory calculators out there often require choosing a queuing model from the Kendall notation before calculating inputs.

Waiting in line is a part of everyday life because as a process it has several important functions. Queues are a fair and essential way of dealing with the flow of customers when there are limited resources. Negative outcomes arise if a queue process isn’t established to deal with overcapacity.
For example, when too many visitors navigate to a website, the website will slow and crash if it doesn’t have a way to change the speed at which it processes requests or a way to queue visitors.
Related: What is an Online Queue System?
Or, imagine planes waiting for a runway to land. When there is an excess of planes, the absence of a queue would have real safety implications as planes all tried to land at the same time.
The importance of queuing theory comes from the fact that it helps describe features of queues, like average wait time, and provides the tools for optimizing queues. From a business sense, queuing theory in operation research informs the construction of efficient and cost-effective workflow systems.
Queuing theory is powerful because the ubiquity of queue situations means it has countless and diverse applications.
Queuing theory has been applied, just to name a few, to:
- Telecommunications
- Transportation
- Logistics
- Finance
- Emergency services
- Computing
- Industrial engineering
- Project management
- Operation research
Before we look at some specific applications, it’s helpful to understand Little’s Law, a formula that helps to operationalize queuing theory in many of these applications.
Do you know the 6 simple rules of queue psychology?

Little’s Law
Little’s Law connects the capacity of a queuing system, the average time spent in the system, and the average arrival rate into the system without knowing any other features of the queue. The formula is quite simple and is written as follows:
or transformed to solve for the other two variables so that:
Where:
- L is the average number of customers in the system
- λ (lambda) is the average arrival rate into the system
- W is the average amount of time spent in the system
Project management processes like Lean and Kanban wouldn’t exist without the Little’s Law queuing models. They’re critical for business applications, in which Little’s Law can be written in plain English as:
Little’s Law gives powerful insights because it lets us solve for important variables like the average wait of in a queue or the number of customers in queue simply based on two other inputs.
A line at a cafe
For example, if you’re waiting in line at a Starbucks, Little’s Law can estimate how long it would take to get your coffee.
Assume there are 15 people in line, one server, and 2 people are served per minute. To estimate this, you’d use Little’s Law in the form:
Showing that you could expect to wait 7.5 minutes for your coffee.

Image by John Yorke
A line in a virtual waiting room
At Queue-it, we show visitors their wait time in the online queue using a queuing model based on Little’s Law, adding in factors to account for no-shows and re-entries:
Where:
- L is the number of users ahead in line
- λ (lambda) is rate of redirects to the website or app, in users per minute
- N is the no-show ratio
- R is the re-entry rate to the queue
- W is the estimated wait time, in minutes
Military process optimization
We can look at a process optimization example from the military, courtesy of Process.st.
In this real-life example, the military needed to determine the ideal amount of time B-2 stealth bombers would be in maintenance. There are only 20 B-2 aircraft and they need to be ready at a moment’s notice. But they require frequent maintenance, which can range anywhere from 18 to 45 days.
Using Little’s Law helps find the balance of aircraft in use versus aircraft under maintenance.

Image by skeeze from Pixabay
Based on flight schedule analysis, it was calculated that three B-2 bombers would be under maintenance at any given time. The rate at which bombers entered maintenance was also calculated to be roughly every 7 days. So:
- L= number of items in WIP (maintenance) = 3
- A= arrival/departure rate = 1 every 7 days = 1/7 days
- W= the average amount of time spent in maintenance = ???
Put into Little’s Law, this leaves us with:
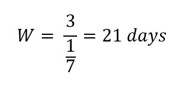
Therefore, the target lead time for B-2 bomber maintenance needed to be 21 days to meet the demands of both available aircraft and the regular flight schedules.
Queuing theory is helpful in explaining the math behind how queues run. But when queues involve humans, queue psychology is important to understand the queue experience as well.
Queue psychology research shows it’s not the length of the wait that determines how positive or negative the queue experience is, but rather how people feel while waiting.
Related: The Psychology of Queuing Revealed in 6 Simple Rules
For example, unoccupied time feels longer than occupied time. Distractions or the ability to do something else while in line makes time feel like it goes by faster. And uncertain waits feel longer than known, finite waits.
That’s why the callback option on customer service lines is so popular. You can feel the anxiety go down when you get the option to be called back in 10 minutes, freeing you to do something else instead of listening to that terrible muzak for an unknown amount of time.
For queuing situations involving people—like websites that use an online queuing system—the psychological rules governing the queues are just as important as the mathematical ones.
(This blog has been updated since it was written in 2020).